Square transformations
In the skillful hands of an inquisitive person, the most ordinary, well-known square becomes an amazing geometric figure.
He can, for example, completely turn into another figure or several other figures of regular or irregular shape. But for each transformation, the square must first be cut into certain parts.
A Chinese scientist Ta-ng cut the square very ingeniously several thousand years ago.
Probably, these parts of the square originally served to demonstrate geometric shapes. In fact, from the parts of this square, you can easily make a rectangle, parallelogram, trapezoid.
Over time, it was noticed that from these parts it was possible to compose many silhouette figures of the most bizarre shape, using all seven parts of the square to compose each figure. This is how an addicting puzzle game was created. which is widespread, especially in its homeland. in China. There this game is known as widely as, for example, we have chess. Even special competitions are arranged to draw up the largest number of figures with the least amount of time. Winners receive special prizes.
I was interested in this idea, and I also tried to create various pictures. silhouettes from the suggested parts of the square. This is how my first acquaintance with the transformation of the square took place. (Application)
Once I came across a puzzle where it was proposed to make three identical squares out of seven parts of a square.
A puzzle square is very similar to a mechanism with well-fitted parts that can be disassembled and assembled into a new mechanism from the same parts. For that. In order to compose the indicated geometric shapes from the finished parts of the square, you do not need any. or calculations and constructions, it is enough to show perseverance, patience, ingenuity and the solution is found.
By adding the figures from the pieces of this puzzle, I saw that you can get not only three identical squares, but also a rectangle made up of these squares.
However, for those who are passionate about mathematics, it is not enough just to add polygons from ready-made parts of a square, but want to learn how to cut a square into parts necessary to compose a particular figure. In other words. give a rationale for the possibility of transforming figures. In the language of geometry, this means: to find those geometric constructions with the help of which the square is cut, and to prove that the required figure can be made from the obtained parts. This formulation of the question immediately turns our puzzle into a more interesting, but also more difficult geometric problem on figures.
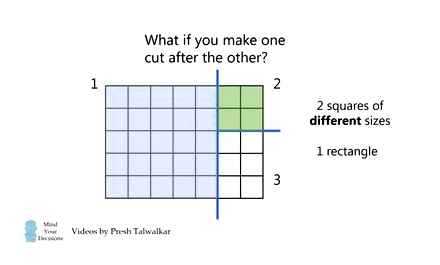
Let’s formulate the puzzle task as a geometric problem:
Show how you need to divide this square with rectangular cuts so that by arranging the resulting parts you can make three solid squares equal to each other.
Finding the Area of a Composite Figure | Area of Composite Rectangles
Nothing is said here about how many parts a given square can be cut into, which means that you can get different solutions to the same problem of reshaping the figure. Thus, when solving problems of this kind, there is a wide opportunity for the manifestation of geometric intuition.
I would like to note that the tasks of transforming one figure into another by rearranging the cut parts were dealt with in ancient times. One of the most remarkable Arab mathematicians, Abul Vefa, who lived in the 10th century, has a number of questions related to the geometric transformation of figures. At one of the meetings of geometers and practitioners, Abul Vefe was proposed just our inverse problem: to make a square of three equal squares.
Let’s get acquainted with the decision made by Abul Vefa. He cut squares 1 and 2 diagonally and attached each of the halves to square 3, as shown in the figure.
Educational Tour
Tasks for independent solution by teams of the “younger” age group
Volume of Open Box Made From Rectangle with Squares Cut Out
The snail crawls up a pillar 10 m high.In a day it rises by 5 m, and during the night it falls by 4 m.How long does it take for a snail to get from the foot to the top of the pillar?
Is it possible to cut a hole in a notebook sheet that a person would crawl through??
Hares are sawing a log. They made 10 cuts. How many blockheads turned out?
Splitting Rectangles into Equal Parts (1.G.3)
The bagel is cut into sectors. 10 incisions were made. How many pieces turned out?
On a large round cake, 10 cuts were made so that each cut goes from edge to edge and goes through the center of the cake. How many pieces turned out?
Two people had two square cakes. Everyone made 2 straight cuts on their cake from edge to edge. In this case, one got three pieces, and the other. four. How could it be?
The hares are sawing the log again, but now both ends of the log are secured. Ten middle blocks fell, and the two outermost ones remained fixed. How many cuts did hares make?
How to divide a pancake with three straight cuts into 4.5, 6, 7 pieces?
There is a round chocolate bar on the rectangular cake. How to cut a cake into two equal parts so that the chocolate is also divided exactly in half?
Is it possible to bake such a cake that can be divided into 4 parts by one straight cut?
What is the maximum number of pieces that a round pancake can be divided into using three straight cuts?
How many times is the staircase to the fourth floor of a house longer than the staircase to the second floor of the same house?
Giuseppe has a sheet of plywood, size 22× 15. Giuseppe wants to cut out of it as many rectangular pieces of size 3× 5. How to do it?
The Magic Land has its own magical laws of nature, one of which says: “A plane carpet will fly only when it has a rectangular shape.”.
Ivan Tsarevich had a flying carpet of size 9 ×12. One day the Serpent Gorynych crept up and cut off a small rug of size 1 from this carpet. ×8. Ivan Tsarevich was very upset and wanted to cut off another piece 1 × 4 to make rectangle 8 ×12, but Vasilisa the Wise suggested doing something differently. She cut the carpet into three pieces, from which she sewed with magic threads a square flying carpet measuring 10× 10.
Can you guess how Vasilisa the Wise remade the damaged carpet??
When Gulliver got to Lilliput, he discovered that all things there are exactly 12 times shorter than in his homeland. Can you tell how many Lilliputian matchboxes fit in Gulliver’s matchbox??
On the mast of a pirate ship, a two-color rectangular flag flies, consisting of alternating black and white vertical stripes of the same width. The total number of stripes is equal to the number of prisoners currently on the ship. At first there were 12 prisoners on the ship, and on the flag there were 12 stripes; then the two prisoners escaped. How to cut a flag in two and then stitch them together so that the area of the flag and the width of the stripes do not change, but the number of stripes becomes 10?
A point was marked in the circle. Is it possible to cut this circle into three parts so that a new circle could be folded out of them, in which the marked point would be in the center?
Is it possible to cut a square into four parts so that each part is in contact (that is, has common sections of the border) with three others?
Assignment 19
The leaf of the calendar is partially covered by the previous torn off leaf (see figure). Tops A and B the upper leaf lies on the sides of the lower leaf. The fourth top of the bottom leaf is not visible. it is covered by the top leaf. The upper and lower leaves, of course, are equal to each other.
Which part of the bottom sheet is larger. closed or open?
12 flags are placed along the treadmill at the same distance from each other. The athlete starts at the first flag and runs at a constant speed. After 12 seconds, the athlete was at the 4th flag. How long does it take to run the entire track?
How long the strip will turn out if a cubic kilometer is cut into cubic meters and laid out in one line?
The inner chambers of the palace of Sultan Ibrahim ibn Said consist of 100 identical square rooms arranged in the form of a square of 10 × 10 rooms. If two rooms have a common wall, then it must have exactly one door. And if the wall is end, then it must have exactly one window. How to count how many windows and doors there are in the chambers of Ibrahim ibn Said?
The distance between Athos and Aramis, galloping along the road, is 20 leagues. In an hour, Athos covers 4 leagues, and Aramis. 5 leagues. What is the distance between them in an hour?
There are no divisions on the 9 cm ruler. Apply three intermediate divisions on it so that it can measure a distance from 1 to 9 cm with an accuracy of 1 cm.
Write some numbers near each vertex of the triangle, write the sum of the numbers at the ends of this side near each side of the triangle. Now add each number near the top to the number near the opposite side. Why do you think the sums are the same??
What is the area of a triangle with sides 18, 17, 35?
Cut the square into five triangles so that the area of one of these triangles is equal to the sum of the areas of the remaining.
A square sheet of paper was cut into six pieces in the shape of convex polygons; five pieces were lost, one piece remained in the shape of a regular octagon (see figure). Is it possible to restore the original square from this octagon alone?
You can easily cut a square into two equal triangles or two equal quadrangles. And how to cut a square into two equal pentagons or two equal hexagons?
Ivan Tsarevich went to look for Vasilisa the Beautiful, kidnapped by Koshchei. Goblin to meet him.
Is he right? How many versts Leshy went and how many Ivan Tsarevich thinks to go?
Come up with a coloring of the sides of the cube so that in three different positions it looks as shown in the picture. (Indicate how to color the invisible edges, or draw a flat pattern.)
Assignment 32
At the numismatist Fedya, all coins have a diameter of no more than 10 cm. He keeps them in a flat box measuring 30 cm 70 cm (in one layer). He was presented with a coin 25 cm in diameter.Prove that all coins can be put in one flat 55 cm 55 cm box.
A central cell was cut out of a 5 × 5 square. Cut the resulting shape into two pieces that can be used to wrap a 2x2x2 cube.
Cut this square along the sides of the cells into four parts so that all the parts are the same size and the same shape and that each part contains one circle and one star.
The parking lot in the Flower City is a 7x 7 squares, in each of which you can park your car. The parking lot is surrounded by a fence, one of the sides of the corner cage is removed (this is the gate). The car drives along a cage-wide track. Dunno was asked to place as many cars as possible in the parking lot so that anyone could leave when the others were standing. Dunno arranged 24 cars as shown in fig. Try to arrange the cars differently to fit more.
Petya and Vasya live in neighboring houses (see the plan in the figure). Vasya lives in the fourth entrance. It is known that Petya, in order to reach Vasya by the shortest route (not necessarily going along the sides of the cages), does not care which side to run around his house. Determine in which entrance Petya lives.
Suggest a way to measure the diagonal of an ordinary brick, which is easy to implement in practice (without the Pythagorean theorem).
Cut a cross made up of five identical squares into three polygons equal in area and perimeter.
A right-angled triangle is given (see figure). Attach a triangle to it (these triangles should have a common side, but should not even partially overlap) so that you get a triangle with two equal sides.
Indicate (draw!) Several different solutions. Each new decision is an additional point.
Petit has three figures cut out of paper. Each of them is white on one side and gray on the other. Which of the five rectangles shown in the figure cannot be added from these figures?
The bodies depicted in the figure are composed of cubes. How many cubes are in each of them?
From the figures in the figure to the task, select those that are unfolding of the cube. Cut them out and show how to glue a cube out of them.
Select the cube corresponding to the given unfolding.
The visible faces of the cube are marked with the numbers 1, 2 and 3. And on the sweeps. two of the named numbers or one. Arrange the numbers 1, 2, 3, 4, 5, 6 on the sweeps of the cube so that the sum of the numbers on opposite sides is 7.
The dashed lines in the figure represent the invisible edges of the cube. Accordingly, the solid lines indicate the visible mowing line. We looked at the cube from the top right. In pictures a, b, c, lay the solid mowing line so that the cube is visible
a) Tetrahedron b) the cube was cut along the edges marked with bold lines (see figures) and unfolded. Draw the resulting sweeps.