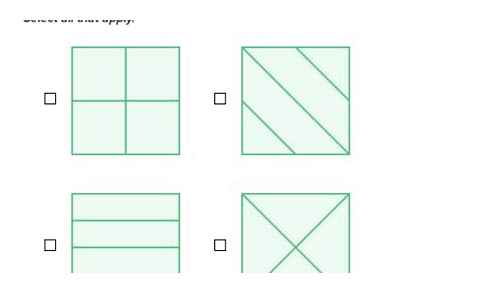
class. 4. Cut a figure into 4 equal parts in area and shape. Answer.
1 6th grade. Oleg wrote a three-digit number on the blackboard, Yegor added the number 5 to its left side, resulting in Yegor’s number was 9 times greater than Oleg’s number. What number did Oleg write? Answer: 65 Directions: x = 9x; x = 65. Peter walks from home to school for 30 minutes, and his brother Sasha walks for 40 minutes. How many minutes later will Peter catch up with Sasha, if Sasha left the house five minutes earlier than Peter? Answer: 0 min. Hint: All the way from home to school, Petya spends 0 minutes less than his brother. So, he will spend 5 minutes less for half of the journey and will meet Sasha exactly halfway from home to school. 3. At the table sat several inhabitants of the island of knights and liars. The traveler asked each of them about their nearest neighbors. Everyone answered: I have both neighbors who are liars. The traveler said: If there were one more or one less, I could find out how many knights among you. But I can’t. What is the smallest possible number of people at the table? Answer: 6. Directions. The knights (P) can only sit at the table one by one between two liars (L), and the liars can either sit one by one or two by two. Therefore, three, four, and five people sitting can arrange themselves in a single way: LRL, RLRL, LRLRL. Six people sitting can arrange themselves in two ways: RLRLRL, RLRLRLRL. 4. A square is divided into 36 smaller squares. Cut it into rectangles along the grid lines in such a way that each rectangle contains exactly one of the indicated numbers. This number must equal the number of squares falling within this rectangle Answer:
2 7th grade. Using no more than 6 digits from, 3, 3, 4, 5, 6, 7, 8, 9, and arithmetic signs and brackets, get the number 06. Each digit can be used no more than once; digits can be combined into numbers. Answer: (68-9)3, 53 A bookstore, when selling a book, made a 0% discount off the original target price and still made an 8% profit. What percent of the profit the store originally expected to make from the sale of the book? Answer: 0%. 90:00 = 08:x; x = Two schoolchildren living in the same house left the house for school at the same time. The first of them walked half of all the time on the way with a speed of 5 km/h, and then walked with a speed of 4 km/h. The second one walked from home to school the first half of the whole distance at a speed of 4 km/h and the second half at a speed of 5 km/h. Which pupil arrived at school first?? Answer: First. 4. Cut the figure into 4 equal parts in area and shape Answer.
3 Grade 8. Two bookstores have the same book on sale. A week later, the first store lowered the price of this book by 0%, and another week later raised it by 0%. In the second store, two weeks later, the price of the book was increased by 0%. In which store, after two weeks, the of the book became lower?? Answer: at the first. Directions. In the first store after two weeks 90 0, and in the second store after two weeks 0 x, x 00 x, 08x Vasya wrote some integers on the board. Petya signed each of Vasya’s numbers with his square. Then Masha added up all the numbers written on the board and got 07. Is it true that one of the guys made a mistake? Answer: Yes. Directions. Suppose none of the guys made a mistake. If Vasya wrote numbers x, x, x n, then Petya should have written numbers x, x. xn. Masha should have counted the sum S x x. xn x x. xn ( x x x ) ( x x ). ( xn xp ). Note that if the number a is an integer, then the number a = a(a ) is even. So, S is the sum of even numbers, so an even number cannot be equal In triangle ABC it is known that A = 5 0, B = SM is perpendicular to side AC and divides side AB into segments AM and MB. Find the ratio of segments AM and BC. Answer: AM : BC =. Note. Let’s mark a point O on AM such that OS = 5 0. Then AO = OS, COM = 30 0 = B; OS = CB; OSM = 75 0 = OMC; OS = OM. Then AM = OS = BC. 4. All positive integers from 64 to 64 are placed arbitrarily in the cells of the chessboard. Is it true that there are two cells adjacent by a side or vertex, the numbers in which differ by at least 9? Answer: True. Suppose the contrary: the difference between the numbers in any two cells adjacent by a side or vertex does not exceed 8. Note that the distance between any two squares does not exceed seven king moves. Therefore the difference between the numbers in any two cells by conjecture does not exceed 78 = 56. But the difference is 64 = 63 56. The resulting contradiction proves, that the assumption is false, and there will be two numbers in the neighboring cells, different no less than by 9.
4 9th grade. For what values of the parameter a do the equations x ax 0 and x x a 0 have a common root? Answer: All students in the school are seated at desks in pairs, and 60% of boys have a boy next to them and 0% of girls have a girl next to them. How many percent of the students in this school are girls? Answer: 00/3% Indication. Let m boys, n girls. The number of boys sitting with girls equals the number of girls sitting with boys, that is, ( 0.6) m = ( 0,) n; 0.4 m = 0.8 n; m = n. Girls are n/(m n) 00% = n/(n n) 00% = 00/3%. 3. In an isosceles triangle ABC B = B inside the triangle, take a point M such that MAB = 0 0 0, MBA = 0 0. Find the CPA. Answer: Directions. The angles at vertex B are 80 0 and 0 0 0. The combination of angles = 60 0 indicates the construction of an equilateral triangle MDB. Triangles ABM and CBD are equal. MAB = DCB, CDB = 50 0, MDC = 50 0, then triangles BDC and MDC are equal. CMMD = CBD = 0 0, BMC = = = Sergey has written in the cells of the table natural numbers from to. Is it true that Oleg can choose two cells adjacent by a side or vertex such that the sum of the numbers in these cells is divisible by 4?? Answer: Correct. Directions. Suppose Oleg cannot choose the two required squares. Replace all the numbers with their remainders when divided by 4. Then there are 484 numbers in the table, that is, 0, and 3 will repeat once each. Let’s break down the table into a table. In each such table there can be no more than one zero and no more than one two. But since the number of tables is equal to the number of zeros and the number of twos, each table has exactly one zero and exactly one two. Note that in each table, the two remaining numbers must both be either ones or threes. But then the number of ones or threes is even, but there is a contradiction.
5 0 class. Make a quadratic equation with roots (a b) and (a b) if a and b are roots of the equation x px q = 0. Answer: x (4q p )x (p 4 4p q) = 0. A right triangle (that is, all vertices of the triangle belong to the parabola) with the hypotenuse parallel to the Oh axis is inscribed in the parabola y = x. Find the height of the triangle dropped on the hypotenuse. Answer: Exhortation. Let A(-x, x ), B(x, x ), C(x, x ) be vertices of triangle ABC. ACB = Point C belongs to a circle with diameter AB. Its equation is x ( y x ) x, so x ( x x x x, whence x x ( 0), that is x x =. ) 3. Let point H be the orthocenter (intersection point of altitudes) of an acute-angled triangle ABC. It is known that NA = BC. Find BAC. Answer: Specifying. BK is the height given to the side of AC. Triangles AHK and BCK are equal (AH = BC, CAN = KBC = 90 0 C), then AK = BK, so right-angled triangle AKB is isosceles and BAC = BAC In Table 4 4, write the natural numbers. Is it true that the sum of the numbers in each following row is 3 more than the previous row, and the sum of the numbers in each following column is 3 more than the previous column? Answer: No. Specifying. Let S be the sum of the numbers in the first row, S the sum of the numbers in the first column. Sum over rows S (S ) (S 4) (S 6) = 4 S = 4(S 3). Sum over stems S (S 3) (S 6) (S 9) = 4 S 8 = 4(S 4) The first sum is divisible by 4, but the second sum is not.
Grade 6. Solve the equation x 3 x 0u = 06 in positive integers Answer: No solution in positive integers. Directions. Consider the residuals modulo 0 of the expressions x 3, 0u and (x 3 x 0u) x y x 3 x 0u So the residual modulo 0 expression gives either 0 or, or 8, which is not equal to 6. So there are no solutions in positive integers. There are 00 shareholders in some company, and any 66 of them together own at least 50% of the company’s shares. What is the highest percentage of all shares one shareholder can own?? Answer: 5% Exhortation. Let M be the shareholder with the largest percentage of shares: x%. Divide the remaining 99 shareholders into three groups A, B, and C of 33 shareholders each. Let them own, respectively, a, b, and c percent of shares. Then (00 x) = (a b c) = (a b) (b c) (a c). i.e. x 5. If each of the 99 shareholders, except M, owns 75% 5% of the shares, then any 66 of them own 50%, and M has exactly 5% of the shares. 3. Express the value of a sin B b sin A through S, where S is the area of triangle ABC; a, b are the sides of triangle ABC; A, B are the interior angles of triangle ABC, lying against the sides of triangle a and b respectively. Answer: 4S Specify. a sinb b sina = a sinb cosb b sina cosa = a b sin A sin B = ab( sin BcosB sin Acos A) = ab( sin BcosB sin Acos A) = b a sin B sin A absin C = ab sin(ab) = ab sinc = 4 = 4S. 4. Suppose there is a grid on the plane and arbitrarily choose 5 points at the nodes of this grid. Is it true that you will find a segment whose ends belong to the chosen nodes and whose midpoint is also a node in this grid?? Answer: Correct. Note. Placing a grid on the coordinate plane. Nodes a point on a coordinate plane with integer coordinates. There are 5 points, and only 4 possible combinations of point coordinates: (even; even), (even; odd), (odd; even), (odd; odd). According to Dirichlet’s principle there are two points with the same parity of coordinates. Since the coordinates of the middle of the segment are expressed by the half-sum of the corresponding coordinates of the ends of the segment, we obtain that the coordinates of the middle of the segment are integers. So the midpoint of this segment is a node in the grid
How to cut a figure into 4 equal parts
A little historical information: Problems of dissection have fascinated many scientists from the earliest times. Solutions to many simple cutting problems were found as early as the ancient Greeks, the Chinese, but the first systematic treatise on the subject belongs to the pen of Aboul-Wefe. Geometers began to seriously consider solving problems on cutting figures into the smallest number of pieces and then constructing another figure at the beginning of the 20th century. One of the founders of this section was the famous founder of puzzles, Henry E.Dewdeny.
Nowadays fans of puzzles are fond of solving dissection problems first of all because there is no universal method of solving such problems, and everyone who sets out to solve them can show their ingenuity, intuition, and creative thinking ability to the full extent. (We will only be pointing out one possible example of a cutscene in the class. It is possible to assume that students may get some other correct combination of.- don’t be afraid of that).
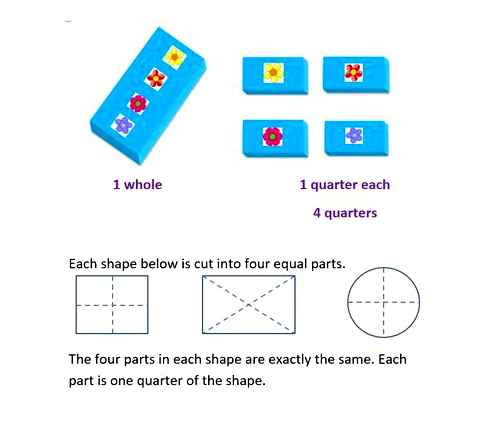
This lesson is supposed to be a hands-on activity. Divide the club participants into groups of 2-3 people. Each group is given figures prepared in advance by the teacher. Students have a ruler (with divisions), pencil, scissors. Only straight cuts may be made with scissors. Having cut some figure into pieces, you need to make another figure from the same pieces.
1). Try to cut the figure shown in the picture into 3 equally shaped pieces:
Hint: The little figures look a lot like the letter T.
2). Now cut this figure into 4 equal-shaped pieces:
Hint: It is easy to guess that the small pieces will consist of 3 squares and there are not many pieces with 3 squares. There are only two kinds: a corner and a rectangle.
3). Divide the figure into two equal parts, and make a chessboard out of the resulting parts.
Hint: Suggest to start the task from the second part, as if to get a chessboard. Recall what shape the chessboard (square) is. Count the available number of cells in length, in width. (Recall that there must be 8 cells.).
4). Try to cut the cheese into eight equal pieces with three strokes of the knife.
Hint: Try to cut the cheese lengthwise.
1). Cut out a square from the paper and do the following:
Cut the cheese into those 4 pieces that can be made into two equal smaller squares.
cut into five pieces. Four isosceles triangles and one square. and fold them so that you have three squares.
3). In front of you are two squares, one of which is already divided into four identical triangles. How to use these triangles and a small square to make one big square? Nothing else needs to be cut.
4). The drawing shows a figure in the form of a comma. Using one curved scythe line, divide this figure into two identical pieces. What geometric figure can be made from these two pieces (“commas”)?
5). One of the sisters of mercy, had five pieces of red cloth, from which she, using all these pieces and not cutting them anymore, has sewed a cross. How she did it?
At the end of the lesson, have the students review the presentation with the tasks. (presentation).
Cut a trapezoid into four equal pieces How to cut an equilateral triangle into four equal pieces can be seen in the figure: If you remove the upper triangle. presentation
2 Cut a trapezoid into four equal pieces How to cut an equilateral triangle into 4 equal pieces can be seen in the figure: If you remove the upper triangle, the remaining 3 triangles will form a trapezoid: Try cutting it into 4 equal pieces too.
3 Cut the “rocket” into four equal parts Cut the figure shown in the picture into 4 equal quadrilaterals:
4 Cutting shapes on checkered paper The drawing represents two shapes. The first of them must be cut into four equal pieces, and the second into five.
5 8 pieces Divide the figure shown into 8 equal pieces. Answer
6 Get the Square Answer Cut the given figure into 3 pieces and make a square out of them. Solve the puzzle in two ways.
7 Of the two squares one There are two 3×3 and 1×1 squares. Cut these squares into pieces that would make one square. If you have solved this problem, try solving it in a general way: rearrange two arbitrary squares into one.
8 Divide a figure into equal parts Try to divide a given figure with broken lines into three equal parts. [ Answer to the puzzle ]Answer to the puzzle
9 Cut this figure into four equal polygons of different shapes from the original figure. [ Answer to the puzzle ] Answer to the puzzle
10 Square In front of you are two squares, one of which is already divided into four identical triangles. How to use these triangles and a small square to make one big square? You do not need to cut anything else. [ Answer to the puzzle ]Answer to the puzzle
Can You Divide The Shape Into 4 Equal Parts?
11 One of the Sisters of Charity, had five pieces of red cloth, from which she, using all these pieces and not cutting them anymore, sewed a cross. How did she do it? [ Answer to puzzle ] Answer to puzzle
12 Cut the figure into four pieces with two cuts and assemble them into a square. [ Answer to the puzzle ] Answer to the puzzle
13 Divide the piece into two equal parts and make a chessboard out of the pieces. [ Answer to the puzzle ] Answer to the puzzle
14 The birthday cake is cut into sixteen identical square pieces. Was it possible to cut the pie into six square pieces (you could even have different sizes)? If possible. how to do it? [ Answer to the puzzle ] Answer to the puzzle
15 The figure shows a figure in the form of a comma. Using one curved mowing line, divide this figure into two equal parts. What geometric figure could be formed from two of these pieces (“commas”)? [ Answer to the puzzle ] Answer to the puzzle
16 How do you cut this cross so that the resulting pieces can be assembled into a square with a void inside it in the form of a cross of the same shape and size. [ Answering the puzzle ] Answer to the puzzle